科学计算 3-24
3.24
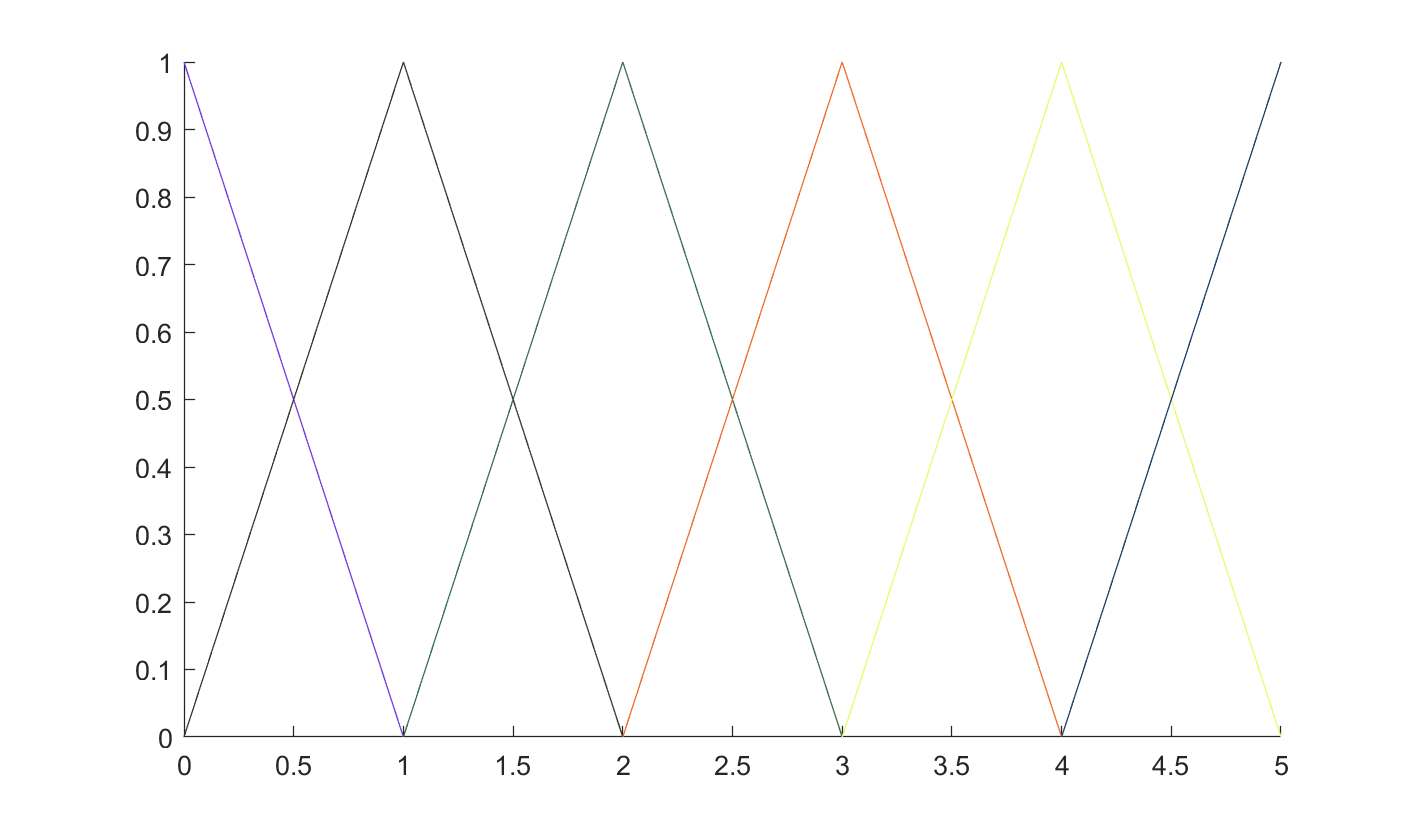
(分段)线性插值基函数的表示
不妨认为直接整数为插值接点
% 可以画图多次(以叠加的方式)
hold on;
% 这个代码默认结点间隔为 1,只需要改下面这一行代码即可
xNode = linspace(0,5,6);
for i=1:length(xNode)
if length(xNode)<2
break;
end
r = rand();
g = rand();
b = rand();
if i == 1
x = linspace(0,xNode(2),100);
y = (x-xNode(2))./(xNode(1)-xNode(2));
plot(x,y,'Color',[r,g,b]);
elseif i == length(xNode)
x = linspace(xNode(i-1),xNode(i),100);
y = (x-xNode(i-1))./(xNode(i)-xNode(i-1));
plot(x,y,'Color',[r,g,b]);
else
x = linspace(xNode(i-1),xNode(i),100);
y = (x-xNode(i-1))./(xNode(i)-xNode(i-1));
plot(x,y,'Color',[r,g,b]);
x = linspace(xNode(i),xNode(i+1),100);
y = (x-xNode(i+1))./(xNode(i)-xNode(i+1));
plot(x,y,'Color',[r,g,b]);
end
end
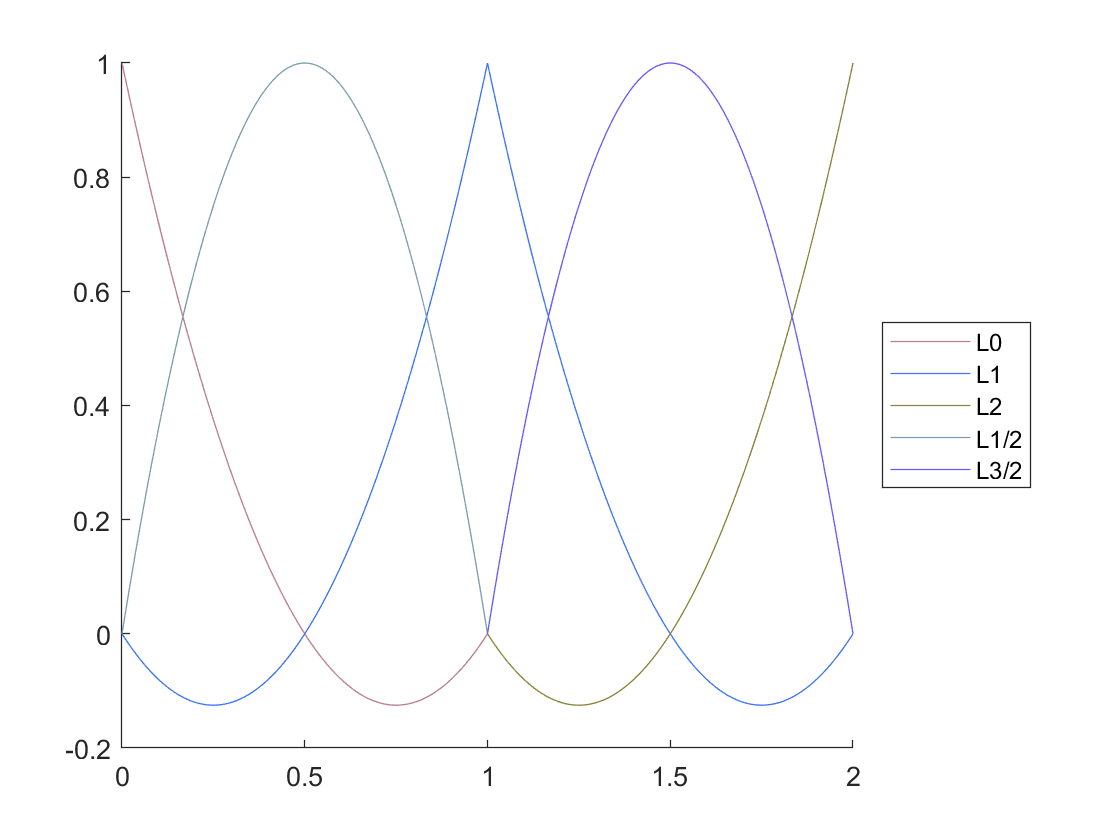
(分段)二次插值基函数的表示
hold on;
xNode = linspace(0,2,3);
for i=1:length(xNode)
if length(xNode)<2
break;
end
r = rand();g = rand();b = rand();
if i == 1
x = linspace(xNode(1),xNode(2),100);
mid1 = (xNode(1)+xNode(2))./2;
y = (x-mid1).*(x-xNode(2))./((xNode(1)-mid1).*(xNode(1)-xNode(2)));
plot(x,y,'Color',[r,g,b],'DisplayName',"L0");
elseif i == length(xNode)
x = linspace(xNode(i-1),xNode(i),100);
mid1 = (xNode(i-1)+xNode(i))./2;
y = (x-mid1).*(x-xNode(i-1))./((xNode(i)-mid1).*(xNode(i)-xNode(i-1)));
plot(x,y,'Color',[r,g,b],'DisplayName',"L"+(i-1));
else
x = linspace(xNode(i-1),xNode(i),100);
mid1 = (xNode(i-1)+xNode(i))./2;
y = (x-xNode(i-1)).*(x-mid1)./((xNode(i)-xNode(i-1)).*(xNode(i)-mid1));
plot(x,y,'Color',[r,g,b],'HandleVisibility','off');
x = linspace(xNode(i),xNode(i+1),100);
mid2 = (xNode(i)+xNode(i+1))./2;
y = (x-mid2).*(x-xNode(i+1))./((xNode(i)-mid2).*(xNode(i)-xNode(i+1)));
plot(x,y,'Color',[r,g,b],'DisplayName',"L"+(i-1));
end
end
for i = 1:length(xNode)-1
%if length(xNode)<2
% break;
% end
r = rand();g = rand();b = rand();
x = linspace(xNode(i),xNode(i+1),100);
mid = (xNode(i)+xNode(i+1))./2;
y = (x-xNode(i)).*(x-xNode(i+1))./((mid-xNode(i)).*(mid-xNode(i+1)));
% DisplayName 指定图例
plot(x,y,'Color',[r,g,b],'DisplayName',"L"+(i*2-1)+"/2");
end
% 对图例位置进行设置
legend('orientation','vertical','location','eastoutside');
hold off;
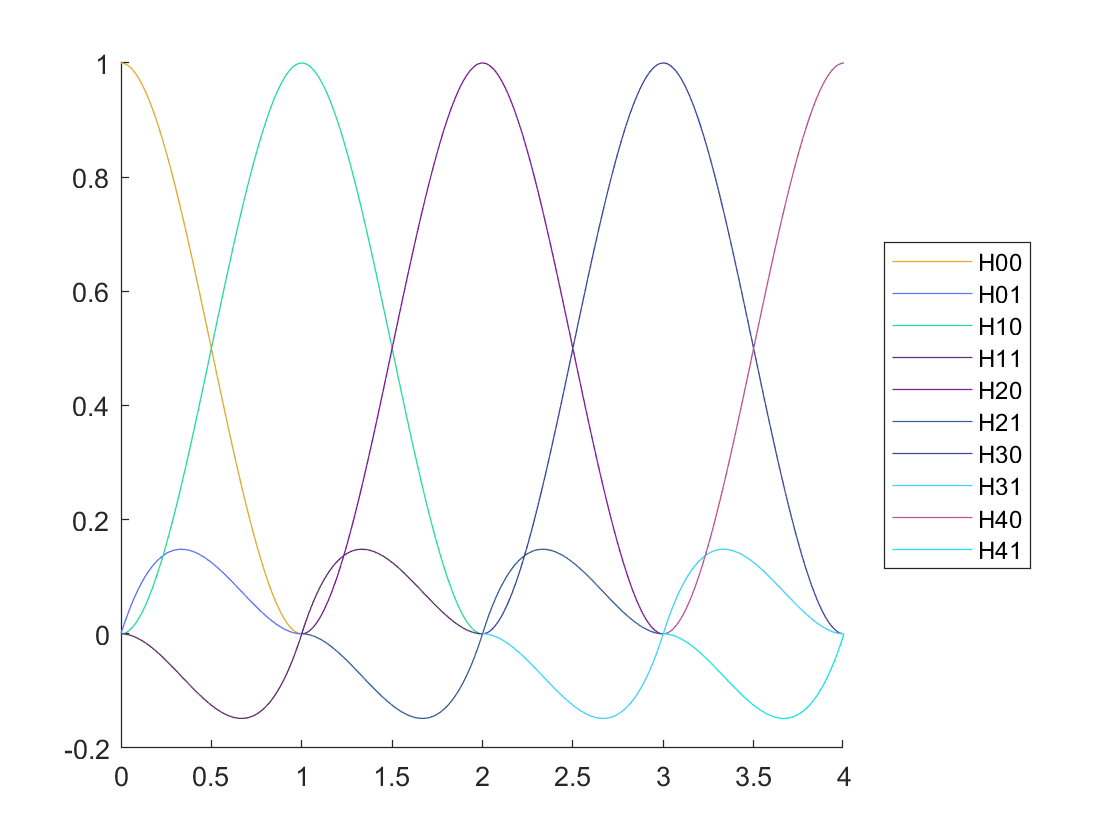
(分段)三次Hermite插值基函数的表示
clf;
hold on;
xNode = linspace(0,4,5);
for i=1:length(xNode)
if length(xNode)<2
break;
end
r = rand();g = rand();b = rand();
if i == 1
x = linspace(xNode(1),xNode(2),100);
y = (1-(x-xNode(1))).^2.*(1+2.*(x-xNode(1)));
plot(x,y,'Color',[r,g,b],'DisplayName',"H"+(i-1)+"0");
r = rand();g = rand();b = rand();
y = (x-xNode(1)).*(1-(x-xNode(1))).^2;
plot(x,y,'Color',[r,g,b],'DisplayName',"H"+(i-1)+"1");
elseif i == length(xNode)
x = linspace(xNode(i-1),xNode(i),100);
y = (x-xNode(i-1)).^2.*(3-2.*(x-xNode(i-1)));
plot(x,y,'Color',[r,g,b],'DisplayName',"H"+(i-1)+"0");
r = rand();g = rand();b = rand();
y = (x-xNode(i-1)).^2.*(x-xNode(i-1)-1);
plot(x,y,'Color',[r,g,b],'DisplayName',"H"+(i-1)+"1");
else
x = linspace(xNode(i-1),xNode(i),100);
y = (x-xNode(i-1)).^2.*(3-2.*(x-xNode(i-1)));
plot(x,y,'Color',[r,g,b],'HandleVisibility','off');
x = linspace(xNode(i),xNode(i+1),100);
y = (1-(x-xNode(i))).^2.*(1+2.*(x-xNode(i)));
plot(x,y,'Color',[r,g,b],'DisplayName',"H"+(i-1)+"0");
r = rand();g = rand();b = rand();
x = linspace(xNode(i-1),xNode(i),100);
y = (x-xNode(i-1)).^2.*(x-xNode(i-1)-1);
plot(x,y,'Color',[r,g,b],'HandleVisibility','off');
x = linspace(xNode(i),xNode(i+1),100);
y = (x-xNode(i)).*(1-(x-xNode(i))).^2;
plot(x,y,'Color',[r,g,b],'DisplayName',"H"+(i-1)+"1");
end
end
legend('orientation','vertical','location','eastoutside');
hold off;
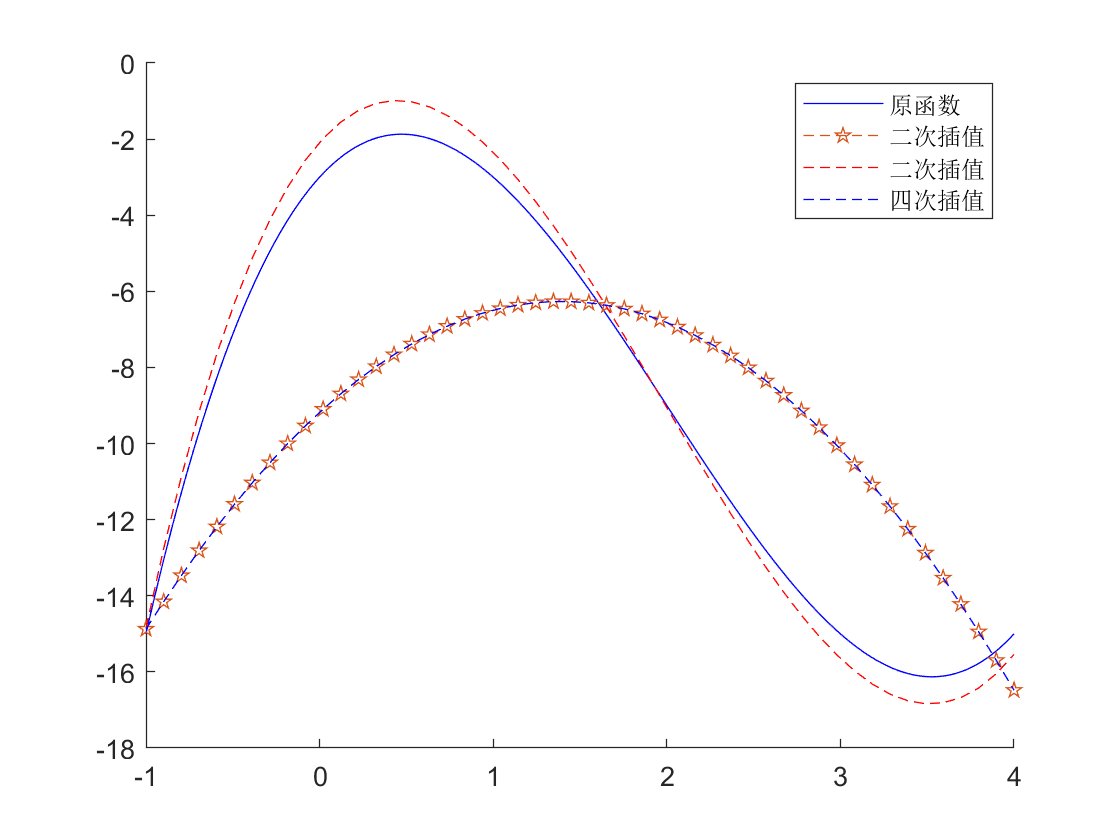
3. $x^3-6x+5x-3$ 上的点做随机扰动后的3次,2次,4次插值
clf;
hold on;
start = -1;
endPoint = 4;
% 原函数图像
x0 = linspace(start,endPoint,1000);
y0 = x0.^3-6.*x0.^2+5.*x0-3;
plot(x0,y0,'b-',"DisplayName","原函数");
% 二次插值
x3 = linspace(start,endPoint,3);
y3 = x3.^3-6.*x3.^2+5.*x3-3;
% 抖动
y3 = y3 + randn(size(y3));
y3 = lagrange(x3,y3,linspace(start,endPoint,50));
plot(linspace(start,endPoint,50),y3,'p--','DisplayName','二次插值');
% 三次插值
x1 = linspace(start,endPoint,4);
y1 = x1.^3-6.*x1.^2+5.*x1-3;
% 抖动
y1 = y1 + randn(size(y1));
y1 = lagrange(x1,y1,linspace(start,endPoint,50));
plot(linspace(start,endPoint,50),y1,'r--','DisplayName','二次插值');
% 四次插值
x2 = linspace(start,endPoint,5);
y2 = x2.^3-6.*x2.^2+5.*x2-3;
% 抖动
y2 = y2 + randn(size(y2));
y2 = lagrange(x2,y2,linspace(start,endPoint,50));
plot(linspace(start,endPoint,50),y3,'b--','DisplayName','四次插值');
legend;
hold off;
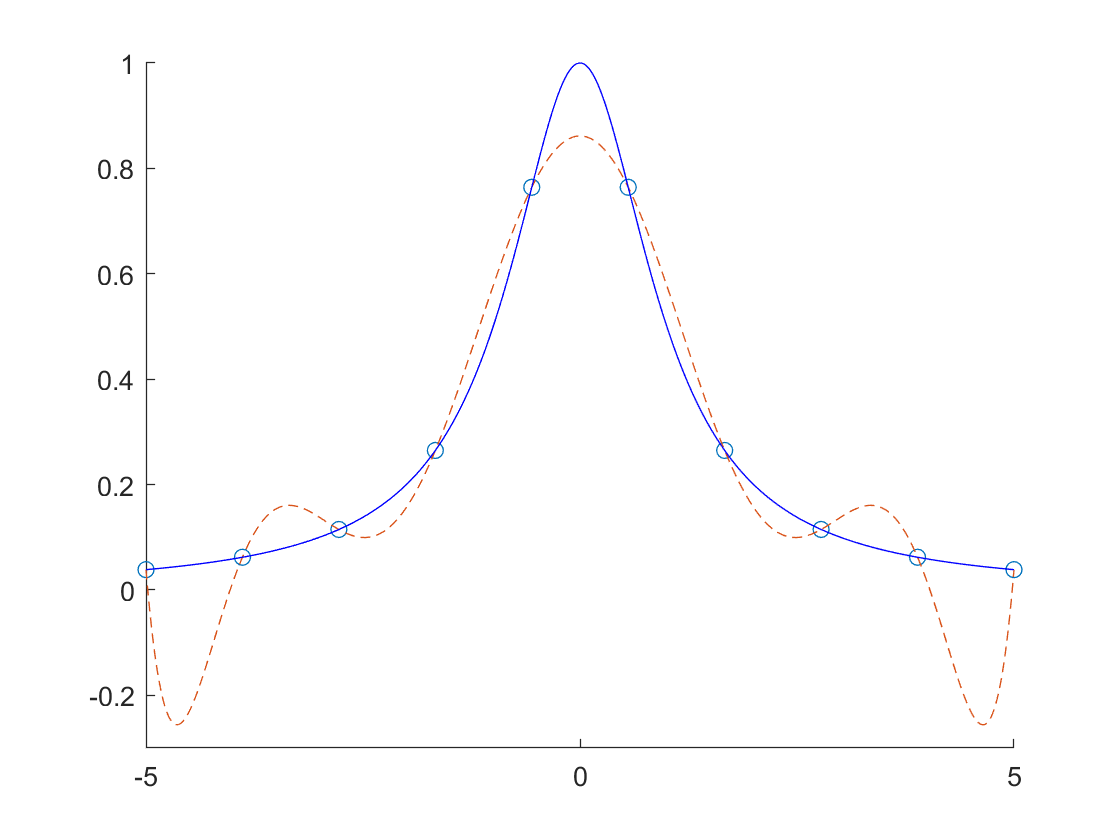
$\dfrac{1}{1+x^2}$ 在 [-1,1] 上高次插值的 Runge 现象
hold on;
x0 = linspace(-5,5,10); % 会有10个点,生成的是9次的多项式
y0 = 1./(1+x0.^2);
plot(x0,y0,'o');
axis([-1 1,0,1]) % 设置坐标轴范围
x1 = linspace(-5,5,1000);
y1 = lagrange(x0,y0,x1);
plot(x1,y1,'--',x1,1./(1+x1.^2),'b-');
axis([-5 5,-0.3 1]) % 设置坐标轴范围
hold off;
这题在 [-1,1] 上现象并不明显。
lagrange.m
function yValue = lagrange(xMatrix,yMatrix,xValue)
% xMatrix 表示插值点中的 x 值
% yMatrix 表示插值点中的 y 值
% xValue 表示希望求的插值多项式的x
% yValue 表示在插值多项式中x对应的函数值
n = length(xMatrix);
yValue = 0;
% i 表示第几个基函数
for i = 1:n
numerator = 1; % 分子
denominator = 1;% 分母
for j=1:n
if i~=j
numerator = numerator.*(xValue-xMatrix(j));
denominator = denominator.*(xMatrix(i)-xMatrix(j));
end
end
yValue = yValue + yMatrix(i).*numerator./denominator;
end
end