4.7

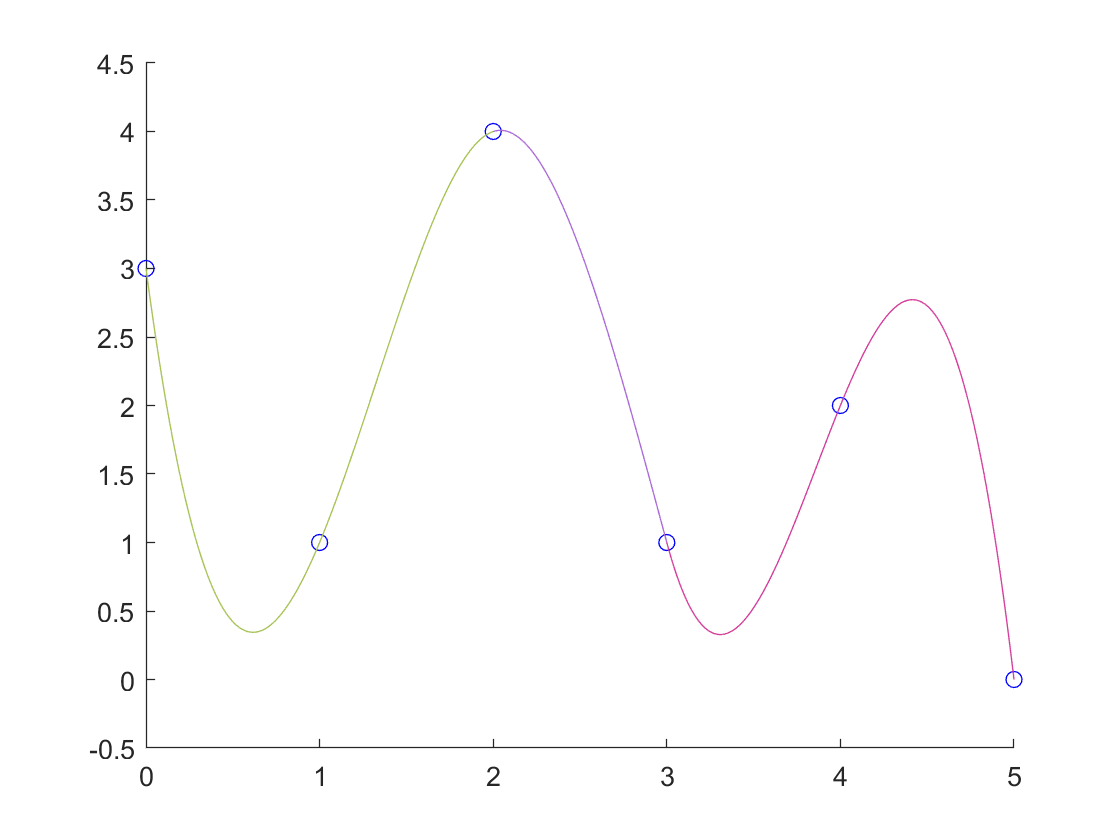
画出过结点 (0,3),(1,1),(2,4),(3,1),(4,2),(5,0) 的三次样条的图像。边条件为：

两端点的二阶导数(特别包括取0值的自然样条)

hold on;
x0 = [0,1,2,3,4,5];
y0 = [3,1,4,1,2,0];
plot(x0,y0,'o');
% 两端点的二阶导数值
secDerLeft = 0;
secDerRight= 0;
% 直接用 csape 函数
% cs0 = csape(x0,y0,'variational');
% yy = ppval(cs0,linspace(0,5,100));
% plot(linspace(0,5,100),yy,'r--');
% [2,2] 表示两个都是二阶导的值
cs = csape(x0,[secDerLeft,y0,secDerRight],[2,2]);
xxt = linspace(-1,6,100);
yyt=ppval(cs,xxt);
plot(xxt,yyt,'r--');
hold off;

图裂了

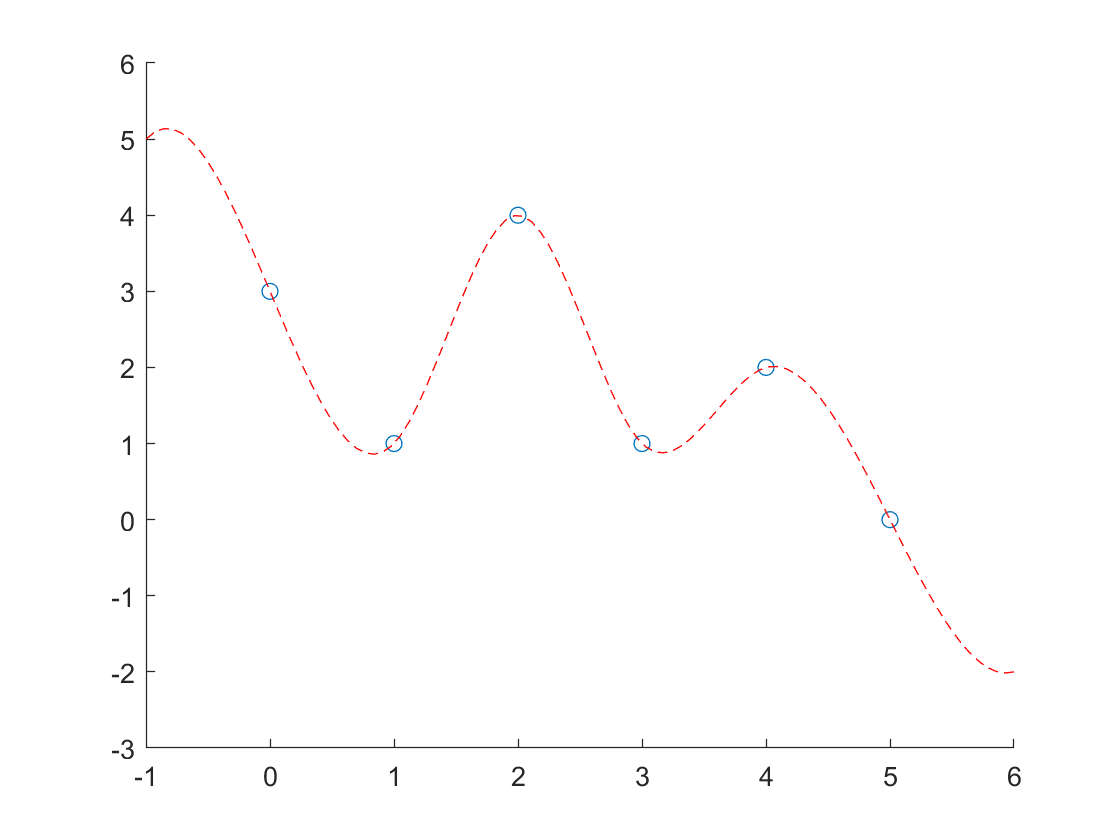
% 改好了
% 默认h_i 恒等于 1
hold on;
x0 = [0,1,2,3,4,5];
y0 = [3,1,4,1,2,0];
plot(x0,y0,'o');
b = zeros(length(x0),1);
A = zeros(length(x0));
for i=2:length(x0)-1
    b(i) = 6.*(y0(i+1)+y0(i-1)-2.*y0(i));
end
A(1,1)=1;
A(length(x0),length(x0))=1;
for i=2:length(x0)-1
    A(i,i-1)=1;
    A(i,i+1)=1;
    A(i,i)=4;
end
m = A\b;
% 可以在这里设置二阶导数值
% 左边的二阶导数值为 m(1) = 左二阶导数值
% m(length(m)) = 右二阶导数值
for i=1:length(x0)-1
    red = rand();green = rand();blue = rand();
    x = linspace(x0(i),x0(i+1),100);
    if i == 1
        x = linspace(x0(i)-1,x0(i+1),200);
    elseif i == length(x0)-1
        x = linspace(x0(i),x0(i+1)+1,200);
    end
    a = y0(i);
    b = y0(i+1)-y0(i)-m(i)./2-(m(i+1)-m(i))./6;
    c = m(i)./2;
    d = (m(i+1)-m(i))./6;
    % x = x-x0(i);
    y = a +b.*(x-x0(i))+c.*(x-x0(i)).^2+d.*(x-x0(i)).^3;
    plot(x,y,'Color',[red,green,blue]);
end
hold off;

图裂了

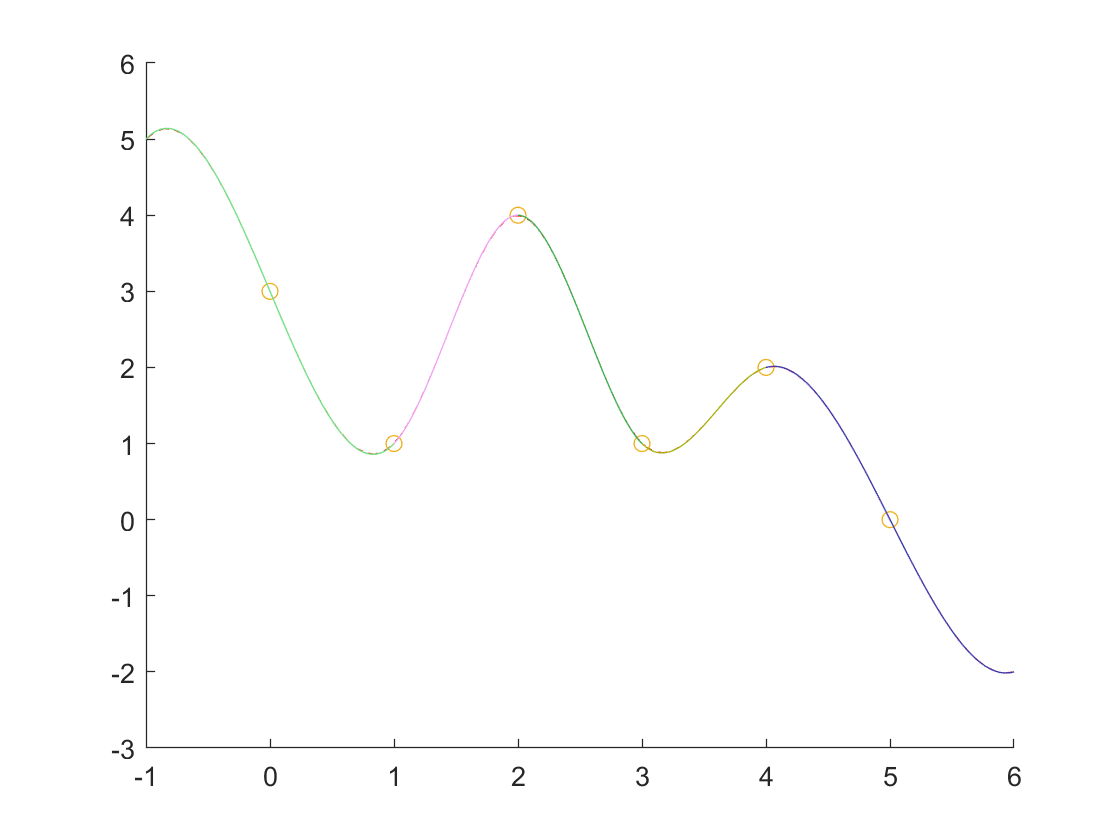
两端点的一阶导数

hold on;
x0 = [0,1,2,3,4,5];
y0 = [3,1,4,1,2,0];
plot(x0,y0,'o');
% 两端点的一阶导数值
derLeft = 0;
derRight= 0;
% 直接用 csape 函数
% [1,1] 表示两个都是二阶导的值
cs = csape(x0,[derLeft,y0,derRight],[1,1]);
xxt = linspace(-1,6,100);
yyt=ppval(cs,xxt);
plot(xxt,yyt,'r--');
hold off;

图裂了

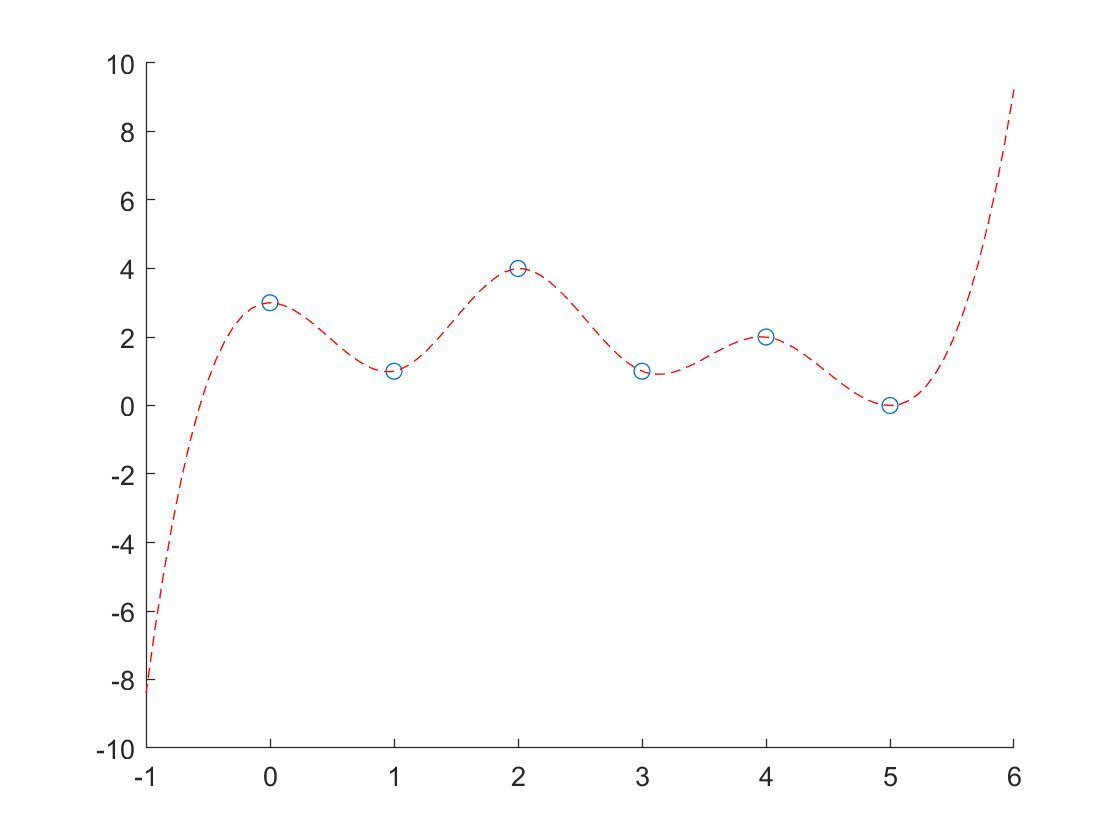
在区间 [0,1] 和 [4,5] 上为二次多项式

设 [0,1] 上为 $S_0(x)=b_0(x-x_0)^2+c_0(x-x_0)+d_0$
设 [4,5] 上为 $S_4(x)=b_4(x-x_4)^2+c_4(x-x_4)+d_4$
设 $[x_{i},x_{i+1}]$ 上为 $S_i(x)=a_i(x-x_i)^3+b_i(x-x_i)^2+c_i(x-x_i)+d_i$
因此 $S_i(x_i) = d_i=y_i$
令 $h_i=x_{i+1}-x_{i}$ 因为这里 $h_i\equiv 1$ 所以就直接用了
$S_0(x_1)=b_0+c_0+d_0=S_1(x_1)=d_1$
$S_i(x_{i+1})=a_i+b_i+c_i+d_i=S_{i+1}(x_{i+1})=d_{i+1}(i=1,2,3)$
$S_0'(x_1)=2b_0+c_0=S_1'(x_1)=c_1$
$S_i'(x_{i+1})=3a_i+2b_i+c_i=S_{i+1}'(x_{i+1})=c_{i+1}(i=1,2,3)$
$S_0''(x_1)=2b_0=S_1''(x_1)=2b_1$
$S_i''(x_{i+1})=6a_{i}+2b_{i}=S_{i+1}''(x_{i+1})=2b_{i+1}(i=1,2,3)$
其实上述都可以合并，只要加一个 $a_0=0,a_4=0$ 即可
设 $m_i=2b_{i}$
$\begin{cases} a_i=\dfrac{m_{i+1}-m_{i}}{6}\
b_i=\dfrac{m_i}{2}\
c_i=y_{i+1}-y_{i}-\dfrac{m_{i+1}-m_{i}}{6}-\dfrac{m_i}{2}(i=0,1,2,3)\
d_i=y_i \end{cases}$
再带入 $3a_i+2b_i+c_i=c_{i+1}(i=0,1,2,3)$
即 $\dfrac{m_{i+1}-m_{i}}{2}+m_i+y_{i+1}-y_{i}-\dfrac{m_{i+1}-m_{i}}{6}-\dfrac{m_i}{2}=y_{i+2}-y_{i+1}-\dfrac{m_{i+2}-m_{i+1}}{6}-\dfrac{m_{i+1}}{2}$

整理可得 $m_{i+2}+4m_{i+1}+m_i=6(y_{i+2}-2y_{i+1}+y_{i})$

其实和固定两端点的二阶导数相同，只需要 $a_0,a_4$ 等于 0 即可，只需要 $b_0=b_1$ 此时 $a_0=0$,$a_4$ 同理

hold on;
x0 = [0,1,2,3,4,5];
y0 = [3,1,4,1,2,0];
plot(x0,y0,'o');
b = zeros(length(x0),1);
A = zeros(length(x0));
for i=2:length(x0)-1
    b(i) = 6.*(y0(i+1)+y0(i-1)-2.*y0(i));
end
A(1,1)=1;
A(length(x0),length(x0))=1;
for i=2:length(x0)-1
    A(i,i-1)=1;
    A(i,i+1)=1;
    A(i,i)=4;
end
m = A\b;
m(1) = m(2);
m(length(m)) = m(length(m)-1);
% 可以在这里设置二阶导数值
% 左边的二阶导数值为 m(1) = 左二阶导数值
% m(length(m)) = 右二阶导数值
for i=1:length(x0)-1
    red = rand();green = rand();blue = rand();
    x = linspace(x0(i),x0(i+1),100);
    if i == 1
        x = linspace(x0(i)-1,x0(i+1),200);
    elseif i == length(x0)-1
        x = linspace(x0(i),x0(i+1)+1,200);
    end
    a = y0(i);
    b = y0(i+1)-y0(i)-m(i)./2-(m(i+1)-m(i))./6;
    c = m(i)./2;
    d = (m(i+1)-m(i))./6;
    % x = x-x0(i);
    y = a +b.*(x-x0(i))+c.*(x-x0(i)).^2+d.*(x-x0(i)).^3;
    plot(x,y,'Color',[red,green,blue]);
end
hold off;

图裂了

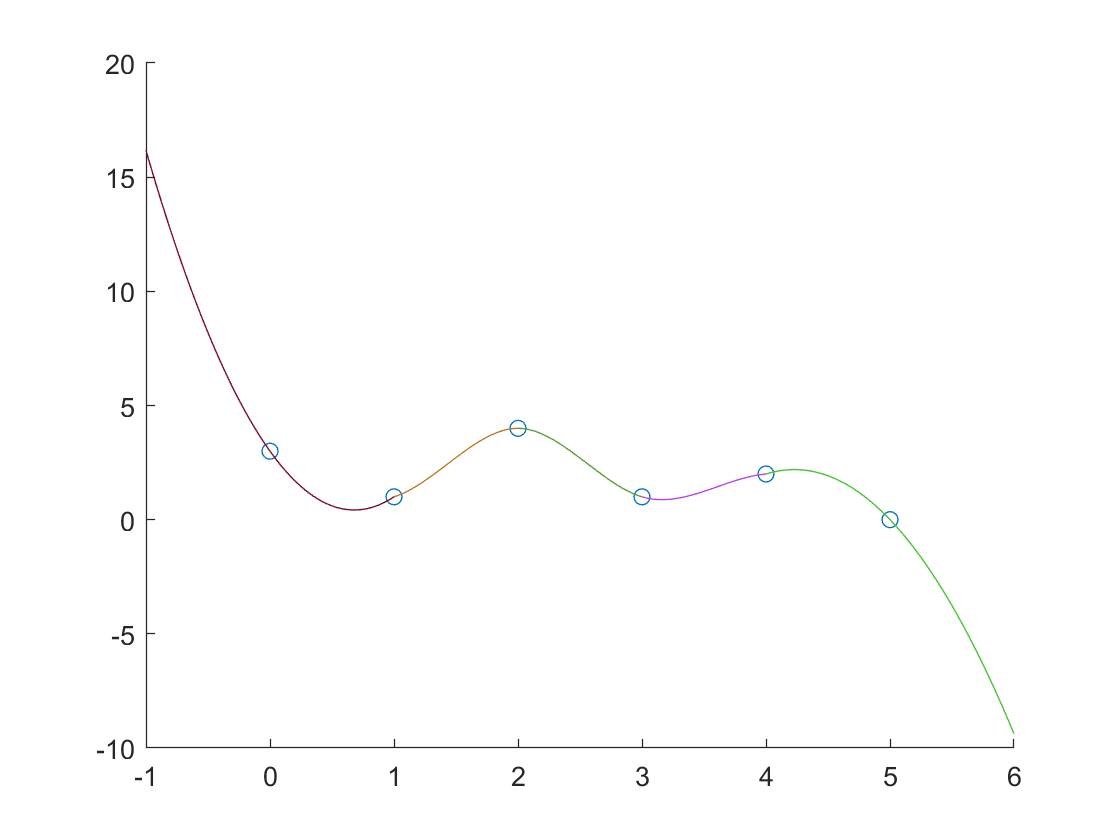
在区间 [0,2] 和 [3,5] 上为三次多项式
一共有三个三次多项式，即
设分别为
$S_0(x)=a_0(x-x_0)^3+b_0(x-x_0)^2+c_0(x-x_0)+d_0$
$S_2(x)=a_2(x-x_2)^3+b_2(x-x_2)^2+c_2(x-x_2)+d_2$
$S_3(x)=a_3(x-x_3)^3+b_3(x-x_3)^2+c_3(x-x_3)+d_3$
$d_0=y_0$
$d_2=y_2$
$d_3=y_3$
$S_0(x_1)=a_0+b_0+c_0+d_0=y_1$
$S_0(x_2)=8a_0+4b_0+2c_0+d_0=y_2=d_2$
$S_2(x_3)=a_2+b_2+c_2+d_2=d_3=y_3$
$S_3(x_4)=a_3+b_3+c_3+d_3=y_4$
$S_3(x_5)=8a_3+4b_3+2c_3+d_3=y_5$
$S_0'(x_2)=12a_0+4b_0+c_0=S_2'(x_2)=c_2$
$S_2'(x_3)=3a_2+2b_2+c_2=S_3'(x_3)=c_3$
$S_0''(x_2)=12a_0+2b_0=S_1''(x_2)=2b_2$
$S_2''(x_3)=6a_2+2b_2=S_3''(x_3)=2b_3$
系数矩阵的行列式大于0，因此有唯一解

x0 = [0,1,2,3,4,5];
y0 = [3,1,4,1,2,0];
A = zeros(12);
b = zeros(12,1);
A(1,4) = 1;  b(1) = y0(1);
A(2,8) = 1;  b(2) = y0(3);
A(3,12)= 1;  b(3) = y0(4);
A(4,1:4)=[1,1,1,1];b(4)=y0(2);
A(5,1:4)=[8,4,2,1];b(5)=y0(3);
A(6,5:8)=[1,1,1,1];b(6)=y0(4);
A(7,9:12)=[1,1,1,1];b(7)=y0(5);
A(8,9:12)=[8,4,2,1];b(8)=y0(6);
A(9,1:3)=[12,4,1];A(9,7)=-1;
A(10,5:7)=[3,2,1];A(10,11)=-1;
A(11,1:2)=[12,2];A(11,6)=-2;
A(12,5:6)=[6,2];A(12:10)=-2;
cof = A\b;
hold on;
indeces = [0,2,3,5];
plot(x0,y0,'bo');
for i=1:length(indeces)-1
    index = indeces(i)+1;
    red = rand();green = rand();blue = rand();
    x = linspace(x0(index),x0(indeces(i+1)+1),(x0(indeces(i+1)+1)-x0(index))*100);
    a = cof(4*i-3);
    b = cof(4*i-2);
    c = cof(4*i-1);
    d = cof(4*i);
    y = a.*(x-x0(index)).^3+b.*(x-x0(index)).^2+c.*(x-x0(index))+d;
    plot(x,y,'Color',[red,green,blue]);
end
hold off;

图裂了