Leetcode 105 从前序与中序遍历序列构造二叉树 // 洛七的摸鱼池塘

105.从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的 中序遍历，请构造二叉树并返回其根节点。

示例 1:

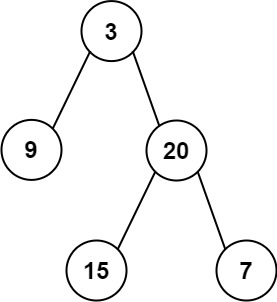
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示：

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列

解答

本题的难度是 Medium.

那根据前序遍历的定义, 前序遍历的第一个节点一定是根节点, 而根据中序遍历的定义, 一个节点的左子树的所有节点一定在这个节点的左边, 右子树的所有节点一定在这个节点的右边. 所以我们可以根据前序遍历的第一个节点, 在中序遍历中找到这个节点, 并且确定这个节点的左右子树的节点数量. 有了这些信息, 我们就可以递归的构建二叉树了.

根据前序遍历找到当前的根节点, 并且得到剩余元素得到左右子树的前序遍历
根据前序遍历和当前的中序遍历

代码如下:

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        TreeNode root = createNode(null, preorder,inorder);
        return root;
    }

    private TreeNode createNode(TreeNode parent, int[] preorder, int[] inorder){
        if(preorder.length==0){return null;}
        // 获取前序遍历的第一个节点
        int nodeVal = preorder[0];
        int splitIndex = -1;
        for (int i = 0; i < inorder.length; i++) {
            if (inorder[i] == nodeVal) {
                splitIndex = i;
                break;
            }
        }
        TreeNode node = new TreeNode(nodeVal);
        if(preorder.length == 1) {return node;}
        // 这里其实写的挺莫名其妙的, 因为这题原来做过, 这个代码是原来写的, 真的很抽象
        if (splitIndex != 0){
            // 得到左子树的前序遍历和中序遍历
            node.left = createNode(node, Arrays.copyOfRange(preorder,1,splitIndex+1),
                Arrays.copyOfRange(inorder, 0,splitIndex));
        } else {
            node.left = null;
        }
        if (splitIndex+1 != preorder.length) {
            // 得到右子树的前序遍历和中序遍历
            node.right = createNode(node, Arrays.copyOfRange(preorder, splitIndex + 1, preorder.length),
                    Arrays.copyOfRange(inorder, splitIndex + 1, preorder.length));
        } else {
            node.right = null;
        }
        return node;
    }
}

虽然解决了问题, 但是时间开销为 8ms, 并且但是由于反复使用 for 循环查找节点值在中序遍历中的位置, 导致时间复杂度较高. 优化后的代码如下:

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        // 这里也是很抽象, 我居然想的是用一个 list 来存储 inorder 的值, 然后用 lastIndexOf 来查找
        ArrayList<Integer> list = new ArrayList<>();
        for (int i = 0; i < inorder.length; i++) {
            list.add(inorder[i]);
        }
        TreeNode root = createNode(null, preorder,list);
        return root;
    }

    private TreeNode createNode(TreeNode parent, int[] preorder, List<Integer> inoder){
        if(preorder.length==0){return null;}
        int nodeVal  = preorder[0];
        int splitIndex = inoder.lastIndexOf(nodeVal);
        TreeNode node = new TreeNode(nodeVal);
        node.left = createNode(node, Arrays.copyOfRange(preorder,1,splitIndex+1), inoder.subList(0,splitIndex));
        node.right = createNode(node, Arrays.copyOfRange(preorder,splitIndex+1,preorder.length), inoder.subList(splitIndex+1,preorder.length));
        return node;
    }
}

但是时间开销减少到了 4ms, 不过这样也只击败了 20.66% 的提交, 这边其实也很明白什么原因, 那就是因为疯狂使用 Arrays.copyOfRange 和 subList, 这两个方法的时间复杂度都是 O(n), 因此这里我改成指针的方式替代.

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        TreeNode root = createNode(null, preorder, inorder, 0, preorder.length, 0 ,preorder.length);
        return root;
    }
    private TreeNode createNode(TreeNode parent, int[] preorder, int[] inorder, int startPre, int endPre, int startIn, int endIn){
        if(endPre-startPre==0){return null;}
        int nodeVal  = preorder[startPre];
        // 这边是分析过程
        // preorder -> [3,9,20,15,7], inorder-> [9,3,15,20,7]
        // nodeVal -> 3 -> splitIndex = 1
        // 仔细想想其实代表的是左边的个数 -> splitIndex - startIn
        // 那传给之后的就是 leftP-> startP+1, startP+1+个数 -> startP + 1 + splitIndex - startIn
        // 右边就是 rightP -> startP + 1 + splitIndex - startIn, endP
        // leftP ->  1,splitIndex + 1
        // rightP -> splitIndex + 1, 5
        // 对于 inorder
        // left ->  startIn, splitIndex
        // right -> splitIndex+1, endIn
        int splitIndex = indexOf(inorder, nodeVal, startIn, endIn);
        TreeNode node = new TreeNode(nodeVal);
        node.left = createNode(node, preorder, inorder,
                startPre+1, startPre + 1 + splitIndex - startIn,
                startIn, splitIndex);
        node.right = createNode(node, preorder, inorder,
                startPre + 1 + splitIndex - startIn, endPre,// preorder 的左右边界
                splitIndex+1, endIn);// inorder 的左右边界
        return node;
    }

    public static int indexOf(int[] arr, int target, int start, int end) {
        for (int i = start; i < end; i++) {
            if (arr[i] == target) { return i; // 找到目标值，返回索引位置}
        }
        return -1; // 没有找到目标值，返回 -1, 实际上应该不会返回 -1
    }
}

这里换成了用指针的方法, 但是还是很抽象, 因为去掉了 Arrays.copyOfRange 和 subList, 但又加回了 indexOf 方法, 导致时间开销只减到了 3ms, 击败了 40.28% 的提交. 那这边的开销主要还是因为 indexOf, 并且可能一个区间可能遍历好多遍, 那我希望只遍历一遍, 就会很自然地想到 HashMap.

import java.util.HashMap;

class Solution {
    private HashMap<Integer, Integer> hashMap = new HashMap<>();
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        for (int i = 0; i < inorder.length; i++) {
            hashMap.put(inorder[i],i);
        }
        TreeNode root = createNode(null, preorder, inorder, 0, preorder.length, 0 ,preorder.length);
        return root;
    }
    private TreeNode createNode(TreeNode parent, int[] preorder, int[] inorder, int startPre, int endPre, int startIn, int endIn){
        if(endPre-startPre==0){return null;}
        int nodeVal  = preorder[startPre];
        int splitIndex = hashMap.get(nodeVal);
        TreeNode node = new TreeNode(nodeVal);
        node.left = createNode(node, preorder, inorder,
                startPre+1, startPre + 1 + splitIndex - startIn,
                startIn, splitIndex);
        node.right = createNode(node, preorder, inorder,
                startPre + 1 + splitIndex - startIn, endPre,
                splitIndex+1, endIn);

        return node;
    }

好好好, 这样时间开销就成功地来到了 1ms, 击败了 99.37% 的提交，这个开销已经很满意了, 不过我还试了一下把 HashMap 换成一个长度为 6001 的数组, 代替 HashMap 的功能, 但是经过测试, 时间开销为 2ms, 说明当前情况下, HashMap 的开销更小.(可能因为节点的数量不多, 但是值的范围很大, 所以 HashMap 的开销更小)