Leetcode 889 根据前序和后序遍历构造二叉树
889. 根据前序和后序遍历构造二叉树
给定两个整数数组, preorder 和 postorder ,其中 preorder 是一个具有 无重复 值的二叉树的前序遍历,postorder 是同一棵树的后序遍历,重构并返回二叉树。
如果存在多个答案,您可以返回其中 任何 一个。
示例 1:
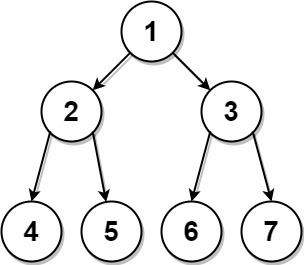
输入: preorder = [1,2,4,5,3,6,7], postorder = [4,5,2,6,7,3,1]
输出: [1,2,3,4,5,6,7]
示例 2:
输入: preorder = [1], postorder = [1]
输出: [1]
提示:
1 <= preorder.length <= 301 <= preorder[i] <= preorder.lengthpreorder中所有值都 不同postorder.length == preorder.length1 <= postorder[i] <= postorder.lengthpostorder中所有值都 不同- 保证
preorder和postorder是同一棵二叉树的前序遍历和后序遍历
Related Topics
- 树
- 数组
- 哈希表
- 分治
- 二叉树
题目链接: link
解答
本题的难度是 Medium.
题目里有一句话,如果答案有多个, 可以返回任意一个. 那为什么会有多个答案呢?我们可以看以下两棵二叉树
1 1
/ \
2 2
/ \
3 3
这两棵树的前序遍历都是 [1,2,3], 后序遍历都是 [3,2,1], 相同的前序遍历序列和后序遍历序列, 但是二叉树的结构是不一样的, 而一个前序遍历序列+中序遍历序列,或后序遍历序列+中序遍历学列可以唯一确定一棵二叉树. 所以之前的答案都是唯一的, 这里可能是多个的.
这题的思路其实和之前的是一样的,根据当前的前序遍历序列确定根节点, 只是这里多一步, 你需要根据子树的根节点去切分出左子树和右子树的范围. 其他都和前两天的一样, 因此就懒得优化了.
代码如下:
class Solution {
private HashMap<Integer, Integer> hashMap = new HashMap<>();
public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {
for (int i = 0; i < postorder.length; i++) {
hashMap.put(postorder[i], i);
}
return createNode(preorder, postorder,
0, preorder.length,
0, postorder.length);
}
private TreeNode createNode(int[] preorder, int[] postorder,
int startPre, int endPre,
int startPost, int endPost) {
if(endPre-startPre <= 0) {return null;}
int nodeval = preorder[startPre];
TreeNode node = new TreeNode(nodeval);
// 这里是因为有可能就没有子树了, 这就是最后一个节点
if (startPre + 1 == endPre) {return node;}
int splitIndex = hashMap.get(preorder[startPre+1]);
node.left = createNode(preorder, postorder,
startPre+1, startPre + 1 + splitIndex - startPost + 1,
startPost, splitIndex+1);
node.right = createNode(preorder, postorder,
startPre + 1 + splitIndex - startPost + 1, endPre,
splitIndex+1, endPost-1);
return node;
}
}
时间开销为 1ms, 击败了 74.03% 的提交.