Leetcode 1008 前序遍历构造二叉搜索树
前序遍历构造二叉搜索树(Construct Binary Search Tree from Preorder Traversal)
返回与给定前序遍历 preorder 相匹配的二叉搜索树(binary search tree)的根结点。
(回想一下,二叉搜索树是二叉树的一种,其每个节点都满足以下规则,对于 node.left 的任何后代,值总 < node.val,而 node.right 的任何后代,值总 > node.val。此外,前序遍历首先显示节点 node 的值,然后遍历 node.left,接着遍历 node.right。)
题目保证,对于给定的测试用例,总能找到满足要求的二叉搜索树。
示例:
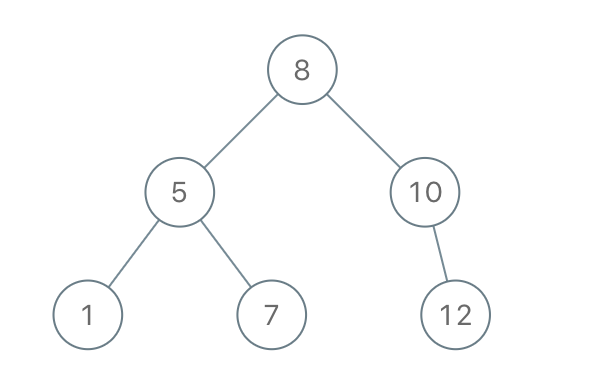
输入:[8,5,1,7,10,12]
输出:[8,5,10,1,7,null,12]
提示:
1 <= preorder.length < = 1001 <= preorder[i] <= 10^8preorder中的值互不相同
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
struct TreeNode* bstFromPreorderRanged(int* preorder, int start, int end){
if(start == end) return NULL;
struct TreeNode* root = malloc(sizeof(struct TreeNode));
root->val = preorder[start];
int i = start+1;
while (i<end && preorder[i]<root->val){
i++;
}
root->left = bstFromPreorderRanged(preorder, start+1, i);
root->right = bstFromPreorderRanged(preorder,i,end);
return root;
}
struct TreeNode* bstFromPreorder(int* preorder, int preorderSize){
return bstFromPreorderRanged(preorder,0,preorderSize);
}
提高效率
int pos;
struct TreeNode* bstFromPreorderRanged(int* preorder, int start, int end, int max){
if(start == end) return NULL;
if(preorder[start] >max) return NULL;
struct TreeNode* root = malloc(sizeof(struct TreeNode));
root->val = preorder[start];
pos++;
root->left = bstFromPreorderRanged(preorder, start+1, end,root->val);
root->right = bstFromPreorderRanged(preorder,pos,end,max);
return root;
}
struct TreeNode* bstFromPreorder(int* preorder, int preorderSize){
pos = 0;
return bstFromPreorderRanged(preorder,0,preorderSize,INT_MAX);
}
少了一个while循环
struct TreeNode* bstFromPreorder(int* preorder, int preorderSize){
struct TreeNode* root = malloc(sizeof(struct TreeNode));
root->val = preorder[0];
root->left = root->right = NULL;
struct TreeNode* path[100];
int topIndex = 0;
path[topIndex] = root;
for(int i=1;i<preorderSize;i++){
struct TreeNode* node = malloc(sizeof(struct TreeNode));
node->val = preorder[i];
node->left = node->right = NULL;
if(preorder[i] < path[topIndex]->val ){
path[topIndex]->left = node;
topIndex++;
path[topIndex] = node;
} else {
while(topIndex-1>=0 && path[topIndex-1]->val <preorder[i]){
topIndex--;
}
if(topIndex -1>=0){
path[topIndex]->right = node;
path[topIndex] = node;
}else{
path[0]->right = node;
path[0] = node;
}
}
}
return root;
}
最后这种方法应该时比较优的解法了