最小路径和(Minimum Path Sum)

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明： 每次只能向下或者向右移动一步。

示例 1： 图裂了

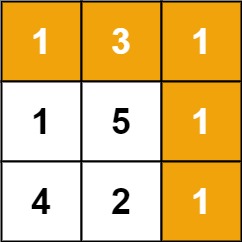
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100

int minPartialPathSum(int** grid,int** path,int ROWS,int COLS,int i,int j){
    if (path[i][j]!=-1){
        return path[i][j];
    }
    int right = grid[i][j];
    int down  = grid[i][j];
    if (i==ROWS-1&&j==COLS-1){
        path[i][j] = grid[i][j];
        return grid[i][j];
    }
    if(j<COLS-1){
         right +=minPartialPathSum(grid,path,ROWS,COLS,i,j+1);
    }
    if(i<ROWS-1){
        down +=minPartialPathSum(grid,path,ROWS,COLS,i+1,j);
    }
    if (j==COLS-1){
        path[i][j] = down;
        return down;
    }
    if (i==ROWS-1){
        path[i][j] = right;
        return right;
    }

    int re = right<down?right:down;
    path[i][j]=re;
    return path[i][j];
}

int minPathSum(int** grid, int gridSize, int* gridColSize){
    int **path = malloc(sizeof(int*)*gridSize);
    for(int i =0;i<gridSize;i++){
        path[i]=calloc(*gridColSize,sizeof(int));
    }
    for(int i =0;i<gridSize;i++){
        for(int j =0;j<*gridColSize;j++){
            path[i][j]=-1;
        }
    }
    int length = minPartialPathSum(grid,path,gridSize,*gridColSize,0,0);
    // 释放内存
    for (int i = 0; i < gridSize; ++i) {
        free(path[i]);
    }
    free(path);
    return length;
}

完全自己写！

老师的代码：

int minPartialPathSum(int ** grid, int row ,int col, int** cache){
    if(row ==0 && col ==0){
        return grid[0][0];
    }
    if(cache[row][col]!=0){
        return cache[row][col];
    }
    int min = INT_MAX;
    if(row-1>=0){
        int upMin = minPartialPathSum(grid, row-1,col,cache);
        if (upMin <min){
            min = upMin;
        }
    }
    if (col-1>=0){
        int leftMin = minPartialPathSum(grid,row,col-1,cache);
        if (leftMin<min){
            min = leftMin;
        }
    }

    cache[row][col] = min +grid[row][col];
    return cache[row][col];
}
int minPathSum(int** grid, int gridSize, int* gridColSize){
    int M = gridSize;
    int N = gridColSize[0];

    int** cache = malloc(sizeof(int*)*M);
    for (int i=0;i<M ; i++){
        cache[i] = calloc(N,sizeof(int));
    }
    int result = minPartialPathSum(grid,M-1,N-1,cache);
    for (int i = 0; i < M; ++i) {
        free(cache[i]);
    }
    free(cache);
    return result;
}

不写递归的话

int minPathSum(int** grid, int gridSize, int* gridColSize){
    int M = gridSize;
    int N = gridColSize[0];

    int** cache = malloc(sizeof(int*)*M);
    for (int i=0;i<M ; i++){
        cache[i] = calloc(N,sizeof(int));
    }
    for (int row = 0; row < M; row++) {
        for (int col = 0; col < N; col++) {
            if(row ==0 && col ==0){
                cache[row][col] = grid[0][0];
                continue;
            }
            int min = INT_MAX;
            if(row-1>=0){
                int upMin = cache[row-1][col];
                if (upMin <min){
                    min = upMin;
                }
            }
            if (col-1>=0){
                int leftMin = cache[row][col-1];
                if (leftMin<min){
                    min = leftMin;
                }
            }

            cache[row][col] = min +grid[row][col];
        }
    }
    int result = cache[M-1][N-1];
    for (int i = 0; i < M; ++i) {
        free(cache[i]);
    }
    free(cache);
    return result;
}

下面这个方法更妙，降低空间复杂度

int minPathSum(int** grid, int gridSize, int* gridColSize){
    int M = gridSize;
    int N = gridColSize[0];

    int** cache = malloc(sizeof(int*)*2);
    for (int i=0;i< 2 ; i++){
        cache[i] = calloc(N,sizeof(int));
    }
    for (int row = 0; row < M; row++) {
        for (int col = 0; col < N; col++) {
            if(row ==0 && col ==0){
                cache[row%2][col] = grid[0][0];
                continue;
            }
            int min = INT_MAX;
            if(row-1>=0){
                int upMin = cache[(row-1)%2][col];
                if (upMin <min){
                    min = upMin;
                }
            }
            if (col-1>=0){
                int leftMin = cache[row%2][col-1];
                if (leftMin<min){
                    min = leftMin;
                }
            }

            cache[row%2][col] = min +grid[row][col];
        }
    }
    int result = cache[(M-1)%2][N-1];
    for (int i = 0; i < 2; ++i) {
        free(cache[i]);
    }
    free(cache);
    return result;
}

巧妙！缩小cache的空间，从O(MN) 变成O(N)